The CUNY Math Challenge

Online Registration is currently CLOSED.

The contest begins on-line at 9:00 A.M. on Monday, February 24, 2020 and ends after an in-person exam at 10 AM on Sunday, March 29, 2020. The contest is composed of two rounds. The first round will take place entirely online remain open for two weeks. The final round, which is by invitation only will consist of an in-person exam.
Round 1

Round 1 will open on Monday, February 24, 2020 at 9:00 A.M. Questions will be posted on the website. Registered participants will have until Sunday, March 8 at 11:59 P.M. to submit their responses for Round 1.

Round 2 will consist of a 120 minutes in-person exam to be held at Baruch College at 10:00 A.M. on Sunday, March 29, 2020. Students will be selected to take the exam based upon their performances in Rounds 1. Selected students will be notified one week in advance of the in-person exam by email. No make-up exam will be administered. All students must present their CUNY IDs to be allowed to sit for the exam.

Answers for Rounds 1 must be submitted online.

Once logged into his/her account, a student will be able to upload individual answer files for each question in the current round. Only PDF file format will be accepted. If the student chooses to handwrite his/her answers, he/she must digitize their answers and save them as separate .pdf files and upload the files to your student’s My Challenge page. Students may resubmit answers as many times as needed but the last submission will always override the previous submission. Each answer file submitted should include their name and Challenge User ID, which was contained in the confirmation email sent at the point of registration. Students are encouraged to use the solution sheet template. Upon successful upload of each answer file, a record of the filename and time of upload will appear on the student’s My Challenge page. If there is no record of the uploaded file on the My Challenge page, there was a problem during the upload; students should resubmit their solutions.

Solutions will be graded based upon several factors including mathematical correctness, supporting arguments, and clarity of presentation. Partial credit may be granted. Carefully written justifications are required for each problem solution. A correct answer without support will receive very little, if any, credit. Scratch work or formulas with no explanation should not be submitted. If a computer calculation is important or central to the solution, the algorithm that has programmed or the procedures employed must be described in some detail (in pseudo-code or otherwise). Source code or executables should not be submitted. The levels of difficulty of the problems in each round varies; some of the questions are very challenging. You don’t need to solve all in a given round to do well.

Rounds will be graded out of twenty points.

A committee of faculty from Mathematics and Computer Science departments across CUNY is responsible for overseeing the scoring. Decisions of the committee are final.

Winners in the final round will get stipend awards ranging from $100 up to a top prize of $500. Winners must have SSN or ITIN in order to receive stipend awards.

70
Suppose that a World Series is completed leading to an extended series where extra exhibition games are played (between the same two teams) after the series has been won. These exhibition games are always to be won by the team that lost the official World Series and are to continue until that losing team also has a total of 4 wins. In this way, if the results of the World Series read ABAABA, then the results of the extended series read ABAABABB.
The sequence of results for the extended series is just an arrangement of 4 copies of the letter A and 4 copies of the letter B. There are 8C4 = 8x7x6x5/4x3x2x1 = 70 such arrangements. (We may choose 4 positions for the letter A from 8 possible positions.)
Each sequence of results for the extended series determines exactly one possible sequence of results for the World Series (by omitting the exhibition games).

Two CUNY math professors arrange to meet to prepare a test. Each will arrive at a random time between 1:00 P.M. and 2:00 P.M. and will wait up to 15 minutes for the other before leaving.
What is the probability that the meeting takes place?

7⁄16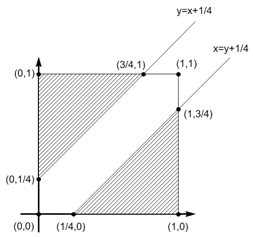

Associate each arrival time between 1:00pm and 2:00pm with a real number r such that 0 < r < 1. The number r represents the part of the hour that has elapsed before the arrival.

In this way the arrival times of the two professors determine a coordinate pair (x,y) that corresponds to a point in the unit square with 0 < x < 1,0 < y < 1.

The pair (x,y) corresponds to a situation where the professors fail to meet if either y > x + 1⁄4 or x > y + 1⁄4 (see right).

In the first of these cases the point (x,y) lies in the triangle that lies above the line y = x + 1⁄4. The area of this triangle is 1⁄2 x 3⁄4 x 3⁄4 = 9⁄32. Similarly, in the second case, the point (x,y) lies in the triangle with area 9⁄32 that lies below the line x = y + 1⁄4. We deduce that the probability that the professors do not meet is 9⁄32 + 9⁄32 = 9⁄16. Therefore the probability that they do meet is 7⁄16.

Alice and Bob are bored and want to play a game. “I have an idea,” Alice chimes in. “How about you flip this coin 2009 times and I’ll flip it 2010 times and whoever gets more Heads wins?” Bob replies, “No, that’s not fair! You’re probably going to win since you get more flips!” “Fine!” answers Alice. “How about this? You flip the coin 2009 times and I’ll flip it 2010 times and if I get more Heads, I win. If you get more Heads, you win. And, if there’s a tie, we’ll say that you win too.” Bob shrugs his shoulders and agrees to play. What’s the probability that Alice wins the game? Prove your answer.

¹⁄₂

1st Proof: Alice flips the coin more often than Bob, so either she must end up with more Heads or with more Tails than Bob. She cannot, however, end up with more Heads and more Tails because she only flips the coin once more than Bob. We deduce that either Alice gets more Heads or she gets more Tails. Since these events are equally likely, both have probability ¹⁄₂.

2nd Proof: Suppose that Alice and Bob begin by flipping the coin N=2009 times each. Let p be the probability that Alice gets more Heads than Bob and let q be the probability that both Alice and Bob get an equal number of Heads. Then 2p+q=1. Alice then flips the coin an (N+1)st time. For Alice to have more Heads, she either had more Heads after the initial Nth flips or an equal number of Heads after the initial flips and her (N+1)st flip must come up Heads. That is, the probability of Alice winning is p+q(1/2). Since 2p+q=1, p+q(1/2)=1/2.